Horizon Based Ambient Occlusion

Введение

В современной компьютерной графике существует множество различных способов расчёта освещения трёхмерной сцены. Самыми базовыми моделями освещения, с которыми знакомится читатель в процессе обучения, являются модель Ламберта, модель Фонга и производные от них модели освещения. Проблема состоит в том, что такие модели являются локальными — при расчете освещённости некоторой точки трёхмерной сцены используется (как правило) позиция этой точки, нормаль в ней, а также позиции источника света и камеры. Таким образом, при расчете освещённости одного объекта никак не учитывается наличие других объектов в сцене.

Другим способом расчёта освещённости является модель затенения, в которой освещённость точки определяется тем, насколько «она закрыта» от источника света другими объектами в сцене. Предполагается, что у нас есть глобальный источник освещения (например небо), и далее чем больше света от может проникнуть к точке, тем более эта точка освещена. Такой способ расчёта освещённости называется ambient occlusion.

Ambient Occlusion

Самым простым способом реализовать такую модель освещения является трассировка лучей: из точки, для которой рассчитывается освещение испускается пучок лучей во все стороны. Чем больше лучей достигнет источника света, тем более освещена точка. Такой метод не применим для компьютерных игр, так как он вычислительно сложный, и не может быть реализован так, чтобы обеспечить необходимое количество кадров в секунду.

В компьютерных играх используются аппроксимации, выдающие приблизительно похожий (более или менее) результат, и позволяющие реализовать их в режиме «real time». Такой аппроксимацией является технология SSAO (screen space ambient occlusion). Предложенная компанией Crytek в 2007 году, эта технология использует карту глубины сцены: для каждой точки оценивается глубина окружающих точек, и итоговая освещённость вычисляется как разница между глубиной текущей точки (для которой производится расчёт) и окружающих её точек трёхмерной сцены. Такой способ расчёта достаточно грубый, и не корректный с точки зрения физики, но он достаточно долго использовался в компьютерных играх, так как давал (при определённых настройках) неплохой результат.

В этой статье рассмотрим другой, более корректный способ аппроксимации ambient occlusion, предложенный компанией NVidia в 2008 году и дающий более корректный и симпатичный результат: horizon-based ambient occlusion (HBAO).

В этой статье частично используется исходный код и терминология из предыдущей статьи про отложенное освещение. Если понятия g-буфера, карты глубины, мировых и view-space координат вам ни о чём не говорит, то рекомендую ознакомиться сначала со статьёй про отложенное освещение.

Теория

Общий случай

В общем случае, для точки трёхмерной сцены P освещённость можно рассчитать по следующей формуле:

В данной формуле интегрирование происходит по единичной полусфере ω, направленной по нормали в точке P.

Функция V является функцией видимости и возвращает 1, если пущенный по определённому направлению из полусферы ω из точки P луч встретит препятствие, и 0 — если не встретит и достигнет источника света.

Функция W является линейной функцией затухания: чем дальше пересечение от точки P, тем менее оно значимо.

Horizon-Based Ambient Occlusion

Суть метода HBAO заключается в поиске максимального угла обзора, который можно построить из точки P без пересечения с геометрией. Чем больше этот угол, тем больше освещена точка. Так приближается функция V из предыдущей формулы. Такой максимальный угол называется горизонтом, и метод, соответственно, называется horizon-based.

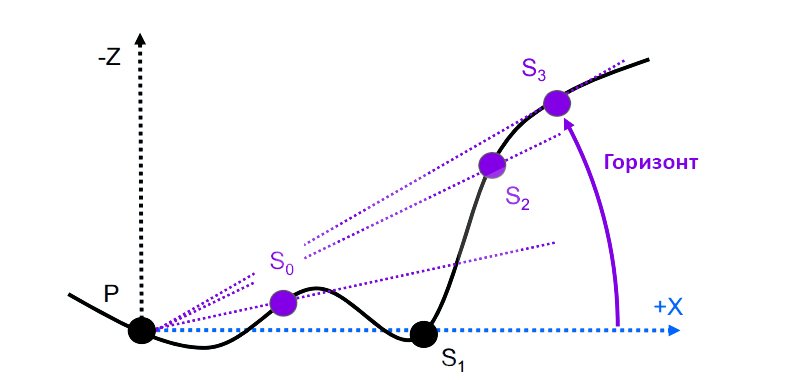
Рассмотрим пример на одномерном изображении:

Алгоритм заключается в пошаговом движении от точки P, для которой рассчитывается освещённость по определённому направлению. На каждом шаге берётся угол между вектором S_iP (где S_i — точка сцены на шаге i) и осью X. Важно заметить, что если на определённом шаге угол меньше чем найденный ранее, то этот шаг пропускается.

Как видно на иллюстрации, на шаге S₁ угол между вектором S₁P и осью X меньше, чем угол между вектором S₀P и осью X, поэтому этот шаг пропускается. На иллюстрации видно, что такая ситуация может возникнуть когда геометрия сцены на шаге S₀ заслоняет собой геометрию на шаге вектором S₁.

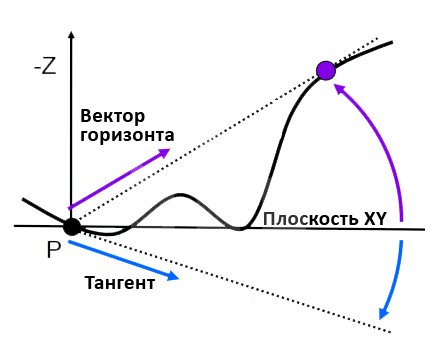
При реальных расчётах вместо оси X будет использоваться плоскость экрана XY, при этом все расчёты ведутся в координатах камеры (view space), в которых точкой отсчёта координат является позиция камеры. Кроме этого следует добавить учёт нормали в точке P в расчётах:

На схеме выше появился вектор тангента (перпендикуляр к нормали). Теперь в расчётах будет использоваться не только угол h (между вектором горизонта и плоскостью XY), но и угол t (между тангентом и плоскостью XY). Логически это можно объяснить так: чем больше угол между нормалью и вектором горизонта, тем более освещена точка. Если же вектор горизонта совпадёт с нормалью в точке, значит эта точка не освещена совсем.

Таким образом, рассмотренную выше формулу для расчёта общего случая ambient occlusion можно переписать следующим образом:

В приведённой выше формуле интегрирование происходит по θ, то есть по всем направлениям (от - π до π). Для каждого направления θ берётся разница между синусом тангента и синусом горизонта. Эта разница домножается на функцию затухания W.

Для упрощения расчёта при практической реализации приведённой выше формулы используется метод Монте-Карло: количество направлений ограничивается, по ним считается сумма подинтегрального выражения, результат делится на количество направлений.

Реализация

Подготовка данных

Входными данными для алгоритма HBAO является g-буфер, содержащий в себе текстуру цвета (albedo), карту запакованных нормалей, карту глубины:

Цвет (albedo)

Запакованные нормали

Карта глубины (х100)

Подготовка g-буфера и передача его в шейдер подробно разобрана в статье про отложенное освещение.

Координаты камеры (view space)

Для удобства все расчёты производятся в пространстве камеры (т.н. view space). Для перевода вектора из пространства мировых координат во view space необходимо умножить этот вектор на матрицу камеры. Получим эту матрицу в скрипте и передадим в шейдер:

Развернуть

Matrix4x4 worldToCameraMatrix = camera.worldToCameraMatrix;
deffered_material.SetMatrix("_worldToView", worldToCameraMatrix);

В шейдере добавим функцию перевода координаты из мирового пространства в пространство камеры:

Развернуть

uniform float4x4 _worldToView;

float3 worldToView(float3 p) {
    float4 result = mul(_worldToView, float4(p, 1.0));
    return result.xyz /result.w;
}

Теперь, всё что необходимо сделать перед расчётом непосредственно ambient occlusion — это перевести координату точки и нормаль в пространство камеры:

Развернуть

float3 pointVS = worldToView(screenToWorld(uv));
float3 normalVS = normalize(mul((float3x3)_worldToView, normal).xyz);

Теперь все данные подготовлены и можно переходить непосредственно к расчёту HBAO. Ниже приложены изображения, которые можно получить если вывести координаты и нормали во view-space пространстве. Если в вашем случае цветовые гаммы сильно отличаются от изображений ниже — вероятно вы ошиблись где-то в расчётах. Рекомендую многократно проверить корректность перевода координат из мирового пространства во view-space — при неверной реализации можно потерять много времени, пытаясь понять почему ничего не работает, или работает некорректно.

Позиции
(view space)

Нормали
(view space)

Надёжным способом проверить корректность перевода координат является реализация освещения по Ламберту во view-space пространстве. Как известно, освещение по Ламберту это, по сути, косинус между нормалью в точке и вектором от точки к источнику света. Соответственно, переведя координату, нормаль и позицию источника света во view-space и посчитав после этого косинус, можно получить корректно рассчитанное освещение по Ламберту. Если освещение выглядит верно и не меняется при движении/поворотах камеры (не прыгает, не сползает и т.д.), значит перевод во view-space у вас работает верно.

Семплирование по одному направлению

Добавим переменные, отвечающие за настройку алгоритма:

radiusSS — максимальная дистанция, на которой ищется горизонт. Указывается в виде дробного числа, где 1.0 - весь экран. При значениях больше 0.25-0.3 алгоритм вменяемо работать не будет.

stepsCount — количество шагов, на которые разбивается radiusSS и в которых ищется угол горизонта. Чем больше это значение, тем более точно работает алгоритм и тем более качественным будет результат....и тем более прожорливым будет алгоритм с вычислительной точки зрения.

deltaUV = float2(radiusSS / (stepsCount + 1.0), 0.0) — двумерный вектор, который будет прибавляться к текстурным координатам в цикле, тем самым обеспечивая движение от исходной точки к максимально удаленной (на radiusSS) от исходной точке. На каждом шаге цикла будет искаться горизонт.

Рассмотрим исходный код, обеспечивающий поиск горизонта и расчёт затухания света occlusion по одному направлению:

Развернуть

// от этого значения будет зависеть чувствительность алгоритма к неровностям
float horizonAngle = 0.04;

// цикл от 1, т.к. при нуле мы получим исходную точку
for (int j = 1; j <= stepsCount; j++) {
    // к текстурным координатам исходной точки добавляем сдвиг
    float2 sampleUV = uv + j * deltaUV;
    // получаем view-space координаты для точки семплирования
    // screen-space -> world-space -> view-space
    float3 sampleVS = worldToView(screenToWorld(sampleUV));
    // строим вектор от точки семплирования к исходной точке (вектор горизонта)
    float3 sampleDirVS = sampleVS - pointVS;
    
    // вычисляем горизонт для точки семплирования: если он меньше чем найденный ранее
    // то ничего не делаем, в противном случае обновляем угол горизонта
    float angle = (PI / 2.0) - acos(dot(normalVS, normalize(sampleDirVS)));  
    if (angle > horizonAngle) {
        float value = sin(angle) - sin(horizonAngle);
        float attenuation = clamp(1.0 - pow(length(sampleDirVS) / 2.0, 2.0), 0.0, 1.0);
        occlusion += value * attenuation;
        horizonAngle = angle;
    }
}

Следует обратить внимание на следующие моменты:

Если на шаге цикла найденный горизонт больше, чем найденный на предыдущем шаге, то разницу между синусами этих углов мы прибавляем к итоговому затуханию, умножив на коэффициент затухания attenuation.
Длина sampleDirVS равна расстоянию от текущей точки семплирования до исходной точки, для которой рассчитывается затухание, и может использоваться для конструирования функции затухания.
Функция затухания, как правило, подбирается вручную. В данном случае это экспонента от sampleDirVS с небольшими коэффициентами для тонкой настройки.
В интернете встречаются реализации, при которых сначала ищется максимальный угол горизонта, а потом occlusion считается на его основе один раз и умножается на функцию затухания. Такой подход является некорректным, т.к. функция затухания (attenuation) будет в таком случае рассчитана один раз, в то время как в нашей реализации она рассчитывается столько раз, сколько раз находится максимальный угол горизонта в процессе прохода по циклу. Таким образом в нашей реализации учитывается тот факт, что чем ближе найденный угол горизонта к исходной точке, тем более значимый вклад он вносит в итоговое затухание света. Это очень важно.

Семплирование по сфере

Нам остался последний шаг: перейти от семплирования по одному направлению к семплированию по сфере. Для этого добавим переменную directionsCount, означающую количество направлений, по которым будет происходить семплирование. Также добавим матрицу поворота deltaRotationMatrix, на которую будет умножаться вектор deltaUV, поворачиваясь тем самым на угол 2π/directionsCount:

Развернуть

const int directionsCount = 64;

float theta = 2.0 * PI / float(directionsCount);
float2x2 deltaRotationMatrix = float2x2(
    cos(theta), -sin(theta),
    sin(theta),  cos(theta)
);

Теперь в шейдере будет два цикла: в одном будет происходить выбор направления, а во втором, вложенном, семплирование по выбранному направлению:

Развернуть

float occlusion = 0.0;

for (int i = 0; i < directionsCount; i++) {
    float horizonAngle = 0.04;

    // поворачиваем каждый раз вектор deltaUV на угол 2PI/directionsCount,
    // переходя таким образом к новому направлению
    deltaUV = mul(deltaRotationMatrix, deltaUV);

    for (int j = 1; j <= stepsCount; j++) {
        float2 sampleUV = uv + j * deltaUV;
        float3 sampleVS = worldToView(screenToWorld(sampleUV));
        float3 sampleDirVS = sampleVS - pointVS;
        
        float angle = (PI / 2.0) - acos(dot(normalVS, normalize(sampleDirVS)));  
        if (angle > horizonAngle) {
            float value = sin(angle) - sin(horizonAngle);
            float attenuation = clamp(1.0 - pow(length(sampleDirVS) / 2.0, 2.0), 0.0, 1.0);
            occlusion += value * attenuation;
            horizonAngle = angle;
        }
    }
}

Остаётся только поделить итоговый результат occlusion на количество направлений (в соответствии с методом интегрирования Монте-Карло), вычесть его из 1 (значение, равное яркости полностью освещённой точки) и донастроить результат с учётом вашей сцены:

Развернуть

occlusion = 1.0 - occlusion / directionsCount;
occlusion = clamp(pow(occlusion, 2.7), 0.0, 1.0);

Итоговый шейдер и результат

Ниже приводится полная версия шейдера, реализующая алгоритм освещения horizon-based ambient occlusion:

Развернуть

Shader "karonator/HBAO" {
    SubShader {
        Cull Off
        ZWrite Off
        ZTest Always

        Pass {
            CGPROGRAM
            #pragma vertex vert_img
            #pragma fragment frag

            #include "UnityCG.cginc"

            uniform sampler2D _Tex0; // color
            uniform sampler2D _Tex1; // normal
            uniform sampler2D _CameraDepthTexture;
            
            uniform float4x4 _clipToWorld;
            uniform float4x4 _worldToView;

            float3 screenToWorld(float2 uv) {
                float depth = tex2D(_CameraDepthTexture, uv).x;
                float4 clipSpacePosition = float4(uv * 2.0 - 1.0, depth, 1.0);
                float4 worldPosition = mul(_clipToWorld, clipSpacePosition);
                return worldPosition.xyz /worldPosition.w;
            }

            float3 worldToView(float3 p) {
                float4 result = mul(_worldToView, float4(p, 1.0));
                return result.xyz /result.w;
            }

            float4 frag(v2f_img input): COLOR {
                const float PI = 3.14159265;

                float2 uv = input.uv;

                float3 pointVS = worldToView(screenToWorld(uv));

                float3 albedo = tex2D(_Tex0, uv).xyz;
                float4 raw_normal = tex2D(_Tex1, uv);
                float3 normal = normalize(2 * (raw_normal.xyz - 0.5));
                float3 normalVS = normalize(mul((float3x3)_worldToView, normal).xyz);

                const float radiusSS = 64.0 / 512.0;
                const int directionsCount = 64;
                const int stepsCount = 32;

                float theta = 2.0 * PI / float(directionsCount);
                float2x2 deltaRotationMatrix = float2x2(
                    cos(theta), -sin(theta),
                    sin(theta),  cos(theta)
                );
                float2 deltaUV = float2(radiusSS / (stepsCount + 1.0), 0.0);

                float occlusion = 0.0;

                for (int i = 0; i < directionsCount; i++) {
                    float horizonAngle = 0.04;
                    deltaUV = mul(deltaRotationMatrix, deltaUV);

                    for (int j = 1; j <= stepsCount; j++) {
                        float2 sampleUV = uv + j * deltaUV;
                        float3 sampleVS = worldToView(screenToWorld(sampleUV));
                        float3 sampleDirVS = sampleVS - pointVS;

                        float angle = (PI / 2.0) - acos(dot(normalVS, normalize(sampleDirVS)));  
                        if (angle > horizonAngle) {
                            float value = sin(angle) - sin(horizonAngle);
                            float attenuation = clamp(1.0 - pow(length(sampleDirVS) / 2.0, 2.0), 0.0, 1.0);
                            occlusion += value * attenuation;
                            horizonAngle = angle;
                        }

                    }
                }

                occlusion = 1.0 - occlusion / directionsCount;
                occlusion = clamp(pow(occlusion, 2.7), 0.0, 1.0);

                float3 outColor = float3(occlusion, occlusion, occlusion);
                return float4(outColor * albedo, 1.0);
            }
            ENDCG
        }
    }
}

Результат:

Horizon-Based Ambient Occlusion

Особенности реализации

Настройка параметров

Алгоритм HBAO очень чувствителен к правильному подбору параметров:

radiusSS — радиус семплирования, указывается в доле от экрана: чем он выше, тем более далёкие объекты будут учитываться при расчёте затенения точки. Обычное значение от 0.05 до 0.15. При значениях больше 0.25 алгоритм будет работать некорректно.
directionsCount и stepsCount — количество направлений по которым проводится семплирование и количество шагов, в которых происходят расчёты для каждого направления. Чем выше эти значение, тем более качественный результат и тем ниже FPS.
начальное значение horizonAngle — в данной статье выбрано как 0.04. В других источниках этот параметр иногда называется как angleBias. Начальное значение горизонта: чем больше это значение, тем меньше алгоритм будет учитывать мелкие детали.
attenuation — функция затухания. Обычно подбирается опытным путём и всегда зависит от расстояния между исходной точкой и точкой семплирования. Чаще всего эта дистанция просто возводится в определённую степень.
Обработка получившегося результата. Итоговое значение occlusion часто тоже возводится в некоторую, подобранную опытным путём степень для увеличения вклада ambient occlusion в итоговый результат.

При неверно подобранных параметрах можно очень легко получить неприемлемый результат при правильной реализации. Хотелось бы ещё раз предостеречь читателей и порекомендовать проверить корректность трансформации координат и нормалей из screen space во view space перед реализацией непосредственно HBAO части алгоритма.

Ускорение алгоритма: шум и размытие

Ускорение алгоритма HBAO достигается за счёт уменьшения параметров directionsCount и stepsCount. Уменьшение этих параметров приведёт к появлению ступенчатости в итоговом результате. Для устранения этого негативного эффекта произвольное значение добавляется к углу поворота deltaUV и точке семплирования. При этом ступенчатость как правило устраняется, но возникает шум, который устраняется обычным размытием (blur) итогового результата освещения.

В данной статье шум и размытие не добавлялись чтобы не переусложнить статью, однако в реальном проекте эти шаги обязательны — в противном случае алгоритм будет слишком прожорлив.

Дальнейшие шаги

Алгоритм HBAO относится к классу screen space алгоритмов: для расчёта результат используется только видимая часть кадра. Это очень, очень серьёзное ограничение: если за пределами видимости камеры есть геометрия, заслоняющая от источника света видимый в кадре объект, то видимый объект будет рисоваться не затенённым. Дальнейшее изучение темы ambient occlusion приведёт читателя к более сложным в реализации, но и более корректным алгоритмам расчёта ambient occlusion: LSAO (Line-Sweep Ambient Obscurance) и GTAO (Ground Truth-based Ambient Occlusion).

Ссылки и файлы

Автор статьи склоняет голову и выражает искреннюю благодарность Богдану Мазуренко aka Che@ter за помощь в разборе теории и практической реализации алгоритма HBAO. В интернете существует большое количество неверных реализаций и всего один документ от компании NVidia, описывающий теоретический базис, лежащий в основе алгоритма. Экспертная помощь Богдана помогла не только корректно реализовать алгоритм, но и разобраться в его тонкостях, чтобы потом поделиться ими с вами.

ambient occlusion HBAO shading

Horizon Based Ambient Occlusion

Введение

Теория

Общий случай

Horizon-Based Ambient Occlusion

Реализация

Подготовка данных

Координаты камеры (view space)

Семплирование по одному направлению

Семплирование по сфере

Итоговый шейдер и результат

Результат:

Особенности реализации

Настройка параметров

Ускорение алгоритма: шум и размытие

Дальнейшие шаги

Ссылки и файлы

Подписаться

Другие статьи