Быстрое построение тепловых карт на Python/Flask/Numba
Постановка задачи
Цель данной статьи - познакомиться с Python библиотекой Numba, позволяющей существенно ускорить написанный на Python код с помощью параллельных вычислений/вычислений с помощью Cuda.
Постановка задачи
Для достижения цели возьмём хорошо подходящую для параллельных вычислений, и в то же время интересно визуализируемую задачу: генерацию тепловых карт. В любой картографической системе карта представляется в виде множества «маленьких кусочков» - тайлов. Обычно первым слоем рисуется непосредственно сама карта (за это мы не отвечаем), а поверх неё уже слой с дополнительной информацией, например, с тепловыми картами.
Алгоритм
- Получить список географических координат всех магазинов перекрёсток в Москве
- Загрузить список адресов всех магазинов с неофициального сайта
- Использовать геокодер гугла для преобразования адресов в географические координаты
- Построить карту доступности магазинов
- Для каждой точки внутри тайла посчитать расстояние до каждого из магазинов
- Основываясь на п.2 построить карту доступности
- Преобразовать карту доступности в цвет (сгенерировать картинку)
- Визуализировать результат с помощью сервиса для работы с картами geojson.io
Неофициальный сайт перекрёстка является сторонним для нас ресурсом, в случае изменения вёрстки код парсера перестанет работать, поэтому рассматривать его надо скорее как пример и шаблон, а не как надёжное, промышленное решение. Ниже приведён скриншот сайта на момент написания статьи. Ниже приведён скриншот сайта в текущий момент времени.
Мы будем считать магазин «доступным», если от исследуемой точки до магазина расстояние не превышает 1.2 км (это расстояние человек проходит за 15 минут).
Подготовка данных
В качестве объекта исследований возьмём сеть магазинов «Перекрёсток» в Москве, и попробуем визуализировать карту доступности этих магазинов в городе.
Обычно тайлы генерируются заранее, после чего уже отдаются тайл сервером, но, т.к. наша задача именно в ускорении расчётов, мы будем делать это «на лету». Чем быстрее будут генерироваться тайлы, тем лучше, меньше будет тормозить отрисовка карты.
Получение списка магазинов
Используя библиотеку aiohttp загрузим страницу, после чего, используя библиотеку BeautifulSoup извлечём из неё адреса магазинов:
async def get_shops_addresses(session):
async with session.get('https://perekrestok-promo.ru/store/g-moskva') as response:
html = await response.text()
tree = BeautifulSoup(html, 'html.parser')
feature = 'Магазин Перекресток по адресу '
raw_links = tree.body.find_all('a', string=re.compile(feature))
links = [(link.text.replace(feature, '')) for link in raw_links]
return linksГеокодинг
На предыдущем шаге мы получили список адресов магазинов. Используя геокодер гугла напишем функцию, которая будет преобразовывать адрес магазина в географические координаты:
async def coordinate_from_address(session, address):
params = [
('key', 'API_KEY'),
('address', address)
]
async with session.get('https://maps.googleapis.com/maps/api/geocode/json', params=params) as response:
text = await response.text()
if response.status == 200:
data = json.loads(text)
try:
position = data['results'][0]['geometry']['location']
return (float(position['lat']), float(position['lng']))
except (KeyError, IndexError):
pass
return NoneИтоговая функция, запускающая (с использованием библиотеки asyncio), сначала, получение списка адресов магазинов, а затем получение координат:
async def load_points():
chunk_size = 30
session = aiohttp.ClientSession()
addresses = await get_shops_addresses(session)
tasks = [coordinate_from_address(session, address) for address in addresses]
results = []
while len(tasks):
chunk = tasks[:chunk_size]
tasks = tasks[chunk_size:]
finished, unfinished = await asyncio.wait(chunk)
results.extend([task.result() for task in finished if task.result() is not None])
await asyncio.sleep(1)
await session.close()
return resultsОбратите внимание, функция отправляет не более 30 запросов к геокодеру одновременно, чтобы не превысить внутреннее ограничение google API на кол-во одновременных запросов.
Генерация тайлов
Знакомство с Numba
Numba — открытая библиотека, использующая для ускорения вычислений технологию JIT, JIT-компиляция, динамическая компиляция — технология увеличения производительности программных систем, использующих байт-код, путём компиляции байт-кода в машинный код непосредственно во время работы программы.
Использование numba начинается с одного из следующих декораторов: njit, vectorize или guvectorize. Рассмотрим кратко каждый из них:
njit
Данный декоратор сообщает что функция должна быть скомпилирована JIT компилятором с использованием флага nopython=True, что, с одной стороны, не позволит использовать в ней внешние переменные и функции, а с другой гарантирует её "быструю" работу (т.к. по сути работать будет скомпилированный код).
vectorize
Данный декоратор применяется к функции, задача которой описать алгоритм, происходящий с одним элементом массива (т.н. скаляром). То есть, если нам надо сложить два массива, то в функции надо будет описать сложение двух чисел, за многократный запуск этой функции для каждого элемента входных массивов, так же как и за паралеллизацию этого процесса будет отвечать Numba.
guvectorize
Самый сложный, и в то же время самый гибкий подход для обработки массивов: входные аргументы являются (как правило), массивами, внутри вы сами работаете с ними и формируете результат. Тут важно обратить внимание, что результат работы функции так же передаётся в неё как входной аргумент. То есть в функцию передаются как входные данные, так и массив, в котором будет заполнен результат (ниже будут рассмотрены примеры).
Рассмотрим пример: приведённая ниже функция рассчитывает расстояние между двумя географическими координатами:
@njit('f8(f8[:], f8[:])')
def dist(point1, point2):
R = 6373.0
lat1, lon1 = point1
lat2, lon2 = point2
delta = point2 - point1
a = math.sin(delta[0] / 2)**2 + math.cos(lat1) * math.cos(lat2) * math.sin(delta[1] / 2)**2
c = 2 * math.atan2(math.sqrt(a), math.sqrt(1 - a))
return R * cФункция выше рассчитывает расстояние между двумя географическими координатами в километрах. Нас интересует описание типов параметров этой функции, указанное в декораторе: f8(f8[:], f8[:]):
f8- float64 число,f8[:]- одномерный массив float64 чисел
Таким образом, функция принимает на вход два массива чисел с плавающей запятой (пары широта/долгота), и возвращает число с плавающей запятой.
Ещё один пример. Функция ниже ограничивает число снизу и сверху (если аргумент меньше задаваемого минимума, возвращает минимум, если больше — возвращает максимум).
@njit('f8(f8, f8, f8)')
def clamp(x, min_val, max_val):
return min(max(min_val, x), max_val)Такие микрофункции при использовании Numba писать, порой, придётся, так как из ускоренных декораторами функций вы не сможете вызывать никакие внешние функции, кроме тех, которые описаны в документации библиотеки.
Генерация сетки
В современных картографических фреймворках карта представляется в виде набора картинок — тайлов. Каждый тайл имеет две координаты, и показывается только на одном уровне детализации (zoom level). Таким образом, тайл характеризуется тремя числовыми значениями (x, y, zoom).
Основываясь на размере тайла и его координате нужно сформировать массив, представляющий собой географические координаты для каждой точки тайла. Отличная задача для параллельных вычислений!
Рассмотрим типы аргументов функции, указанные в декораторе:
-
zeros: Пустой трёхмерный массив float64, нужный для указания размерности аргумента result (об этом ниже). Трёхмерный он, так как для каждой точки в тайле (а это уже два измерения) рассчитывается широта и долгота. К примеру, элемент [10][10][1] означает долготу для точки в тайле с координатой 10, 10.
-
x_range, y_range: Одномерные массивы float64 чисел — диапазоны координат для каждого тайла. К примеру, если мы имеем тайл с координатами x = 3 и y = 4, и размером 10 на 10 пикселей, то получим x_range = [3, 3.11, 3.22 ... 4], y_range = [4, 4.11, 4.22 ... 5].
-
zoom: float64 число — уровень детализации для обрабатываемого тайла.
-
result: Трёхмерный массив float64, в котором будет заполнен результат работы функции. Всё то же самое что и с zeros, только если массив zeros является «входным» аргументом, и нужен, только чтобы сообщить JIT компилятору размерность массива result, то result - это уже «выходной» аргумент с результатами работы функции.
Второй аргумент декоратора guvectorize - сигнатура, жёстко задающая зависимость размерности входных и выходного аргументов:
(a, b, c), (a), (b), () -> (a, b, c)
Обратите внимание, казалось бы, мы знаем что
свсегда равно двум (широта и долгота), и, кажется, могли бы указать в сигнатуре что-то примерно такое:(a), (b), () -> (a, b, 2), избавившись от аргумента zeros. Однако так сделать не получится, и это одно из неприятных ограничений библиотеки Numba. Числа в сигнатуре указывать нельзя, только переменные. Таким образом, чтобы указать размерность выходного аргумента, мы передаём в функцию пустой аргумент с такой же размерностью.
Ниже приведённая функция рассчитывает географические координаты для каждой точки в тайле:
@guvectorize(['void(f8[:, :, :], f8[:], f8[:], f8, f8[:, :, :])'],
'(a, b, c), (a), (b), () -> (a, b, c)',
target='parallel', nopython=True)
def calc_grid(zeros, x_range, y_range, zoom, result):
tile_count = 2.0 ** zoom
for i, x in enumerate(x_range):
for j, y in enumerate(y_range):
lon = x / tile_count * 2 * math.pi - math.pi
lat = math.atan(math.sinh(math.pi * (1 - 2 * y / tile_count)))
result[j][i] = (lat, lon)Обратите внимание на дополнительные флаги в декораторе:
target = parallelозначает «считать на всех доступных ядрах». Вместоparallelможет быть указанаcuda, что даст ещё больше производительности, т.к. для расчётов будет использоваться видеокарта.
nopython = Trueпо сути, указание этого флага включает ускорение. В документации Numba говорится, что указание этого флага равнымFalseпереключит компилятор в режим "object mode", в котором будут доступны python объекты, но производительность не будет превышать производительность обычных python функций.
Поиск расстояний, построение карты доступности
Выше мы рассчитали географические координаты для каждого тайла, сформировали массив с географическими координатами точек интереса (в нашем случае это географические координаты магазинов), и описали функцию, позволяющую рассчитать расстояние между двумя точками.
Основываясь на том, что 1.2 км — расстояние, которое человек может пройти за 15 минут, рассчитаем для каждой точки тайла кол-во доступных магазинов. После этого, преобразуем это кол-во в значение «доступности». Будем считать за «идеальную» доступность ситуацию, при которой в точке доступно 4 и более магазина (значение подбирается вручную, и, по своей сути является аналогом нормализации):
@guvectorize(['void(f8[:, :, :], f8[:, :], f8[:, :])'],
'(n, m, k), (a, b) -> (n, m)',
target='parallel', nopython=True)
def calc_dists(positions, points, result):
for i in range(positions.shape[0]):
for j in range(positions.shape[1]):
buffer = 0
for point in points:
cur_dist = dist(positions[i][j], point)
# копим значение доступности магазинов
# чем магазин ближе, тем больший вклад он внесёт, если дальше чем 1.2 км
# считаем его недоступным, а его вклад в карту доступноти нулевым
buffer += max(0, 1.2 - cur_dist)
result[i][j] = min(1, buffer / 4)Преобразование данных в цвет
Последний шаг в визуализации тайлов — преобразования значения доступности в цвет. В обычной ситуации можно было бы использовать функцию colormap библиотеки matplotlib. Однако, как уже говорилось выше, мы не можем использовать сторонние библиотеки в функциях, ускоренных декораторами numba.
Решение простое — найти реализацию нужной цветовой схемы в исходном коде библиотеки matplotlib и повторить в рамках экосистемы Numba. Я выбрал цветовую схему jet:
Ниже приведённая функция преобразовывает значение доступности в цвет. Обратите внимание на сигнатуру в декораторе. В ней указывается, что входной и выходной массивы имеют одинаковую размерность. Логически это странно, ведь доступность это одно число, а цвет - четыре.
После построения карты доступности мы меняем массив из 256x256 на 256x256x4, что позволяет нам сообщить в декораторе размерность итогового массива. Доступность при этом записывается в первый компонент каждого элемента входного массива.
Пример для понимания:
- Исходная карта доступности:
A = 256x256→A[i][j] = val - Расширенная карта доступности:
A = 256x256x4→A[i][j] = (val, 0, 0, 0)
@guvectorize(['void(f8[:, :, :], f8[:, :, :])'],
'(n, m, k) -> (n, m, k)',
target='parallel', nopython=True)
def calc_colors(dists, result):
for i in range(dists.shape[0]):
for j in range(dists.shape[1]):
x = dists[i][j][0]
r = clamp((4.0 * x - 1.5) if x < 0.7 else (-4.0 * x + 4.5), 0, 1)
g = clamp((4.0 * x - 0.5) if x < 0.5 else (-4.0 * x + 3.5), 0, 1)
b = clamp((4.0 * x + 0.5) if x < 0.3 else (-4.0 * x + 2.5), 0, 1)
a = clamp(dists[i][j][0] * 2, 0, 0.95)
result[i][j] = (r, g, b, a)
result *= 255Итоговая функция генерации тайла
Теперь, когда все детали конструктора реализованы, осталось только сложить их в правильном порядке. Ниже приводится функция, генерирующая для заданного тайла карту доступности в виде PNG изображения, которое можно потом наложить на карту как слой.
def gen_tile(zoom, x, y, points):
size = 256
rng = np.linspace(0, 1, size)
grid = np.zeros((size, size, 2))
# строим координатную сетку (гео координаты для каждой точки тайла)
calc_grid(grid, x + rng, y + rng, zoom, grid)
# переводим координаты точек интереса в радианы (проще будет считать расстояния)
points = np.radians(points)
# рассчитываем карту доступности
dists = np.zeros((size, size))
calc_dists(grid, points, dists)
# делаем из неё трёхмерный массив
dists = np.dstack((
dists.reshape((size, size, 1)),
np.zeros((size, size, 3))
))
# заводим пустой массив для цветов, рассчитываем цвета
colors = np.zeros_like(dists)
calc_colors(dists, colors)
# формируем изображение
image = Image.fromarray(colors.astype('uint8'))
filename = 'files/{z}/{x}/{y}.png'.format(z=zoom, x=x, y=y)
if not os.path.exists(os.path.dirname(filename)):
os.makedirs(os.path.dirname(filename))
image.save(filename)
return filenameРезультат
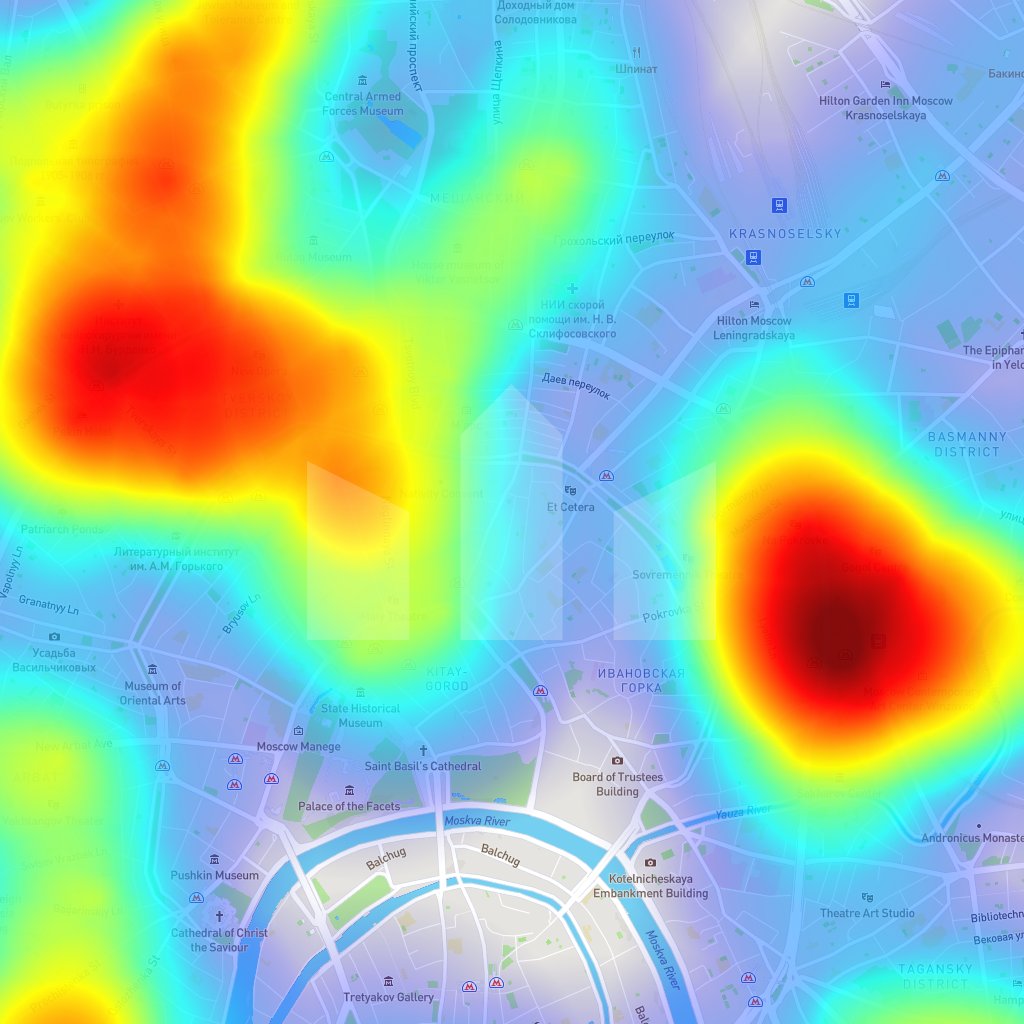
Карта доступности магазинов «Перекрёсток» в Москве
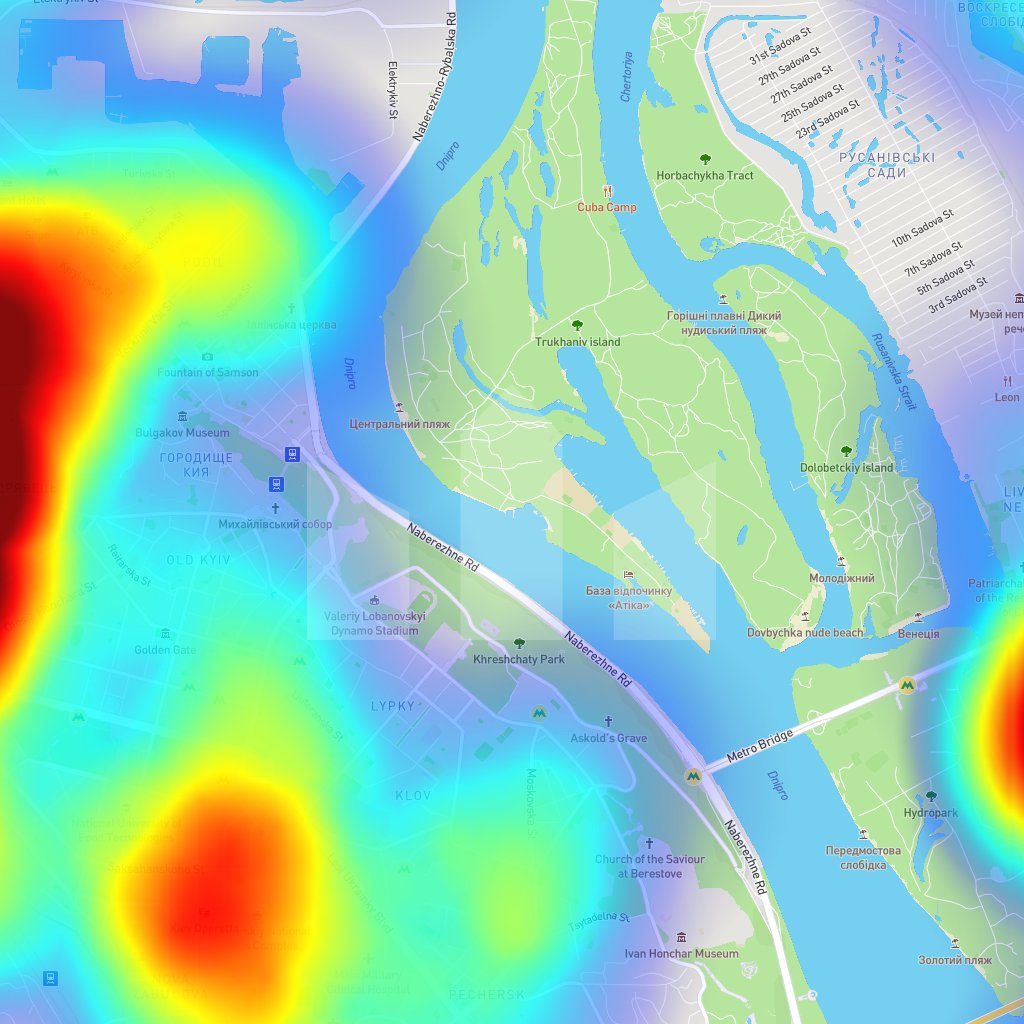
Карта доступности почтовых отделений в Киеве
Оптимизация
Бонусная часть! Давайте выбросим из обработки те точки интереса, которые не внесут никакого вклада в итоговый результат тайла.
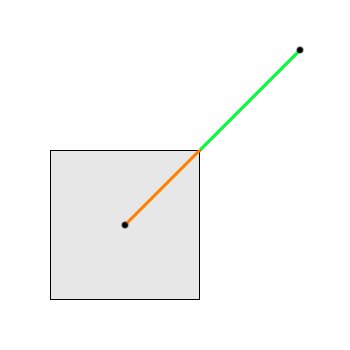
Для этого проверить для каждой точки следующее условие: расстояние от точки интереса до самой ближайшей точки на тайле должно превышать барьерное расстояние (1.2км). Проверить это проще всего, вычтя из расстояния от точки интереса до центра тайла расстояние от точки интереса до границы тайла (см. картинку ниже).
Данный простой кусочек кода может очень сильно ускорить функцию генерации тайла, так как сначала мы исключаем из обработки все точки, которые не повлияют на тайл вообще, и уже потом получившийся массив влияющих на тайл точек используется для построения карты доступности.
filtered_points = []
for point in points:
if (dist(point, grid[128][128]) - dist(grid[0][0], grid[128][128])) < 1.2:
filtered_points.append(point)