Небо как в Crysis: атмосферное рассеяние
Введение
Визуализация неба и атмосферных эффектов - одна из важнейших задач в современной компьютерной графике. В играх с помощью неба передаётся не только время дня, но и настроение, атмосфера, погода.
Кроме этого, цвет неба оказывает влияние на итоговый цвет объектов в сцене: чем дальше объект (или часть ландшафта) от наблюдателя, тем более цвет неба будет заменять цвет объекта. Этот эффект был впервые описан Леонардо да Винчи и называется пространственной перспективой («aerial perspective»). Люди подсознательно используют этот эффект для оценки расстояния до наблюдаемых объектов.
В этой статье будут рассмотрены физические законы, формирующие привычные для нас цвета атмосферы Земли в разное время суток. Далее эти законы будут применены для реализации шейдера неба. Хотелось бы обратить внимание читателей на два момента:
- В интернете большое количество статей, посвящённых атмосферному рассеянию, и максимально подробно описывающих теоретическую часть вопроса. В этой статье основной акцент будет сделан именно на практическую реализацию, теория будет описана в минимальном виде, необходимом для понимания принципов формирования итогового алгоритма и результатов его работы.
- В этой статье рассматриваются только эффекты атмосферного рассеяния «atmospheric scattering» и пространственной перспективы «aerial perspective». Визуализация облаков, являющихся, вообще говоря, неотъемлемой частью неба, будет рассмотрена в следующей статье.
Теория
Атмосфера планеты
Современная компьютерная графика в большинстве своём полигональная. Трёхмерные модели представляются в виде множества полигонов, которые в итоге выстраиваются в сетку (mesh). Далее сетка текстурируется, и освещается. Фактически, для визуализации трёхмерного объекта визуализируется его поверхность. Этот подход хорошо работает для объектов, в которых не может распространяться свет. Но что делать, если материал, из которого сделан объект, может пропускать свет? Хорошим примером является воск: свет огня от свечи может проходить сквозь воск, подсвечивая его изнутри. Такой эффект называется подповерхностным рассеиванием (subsurface scattering).
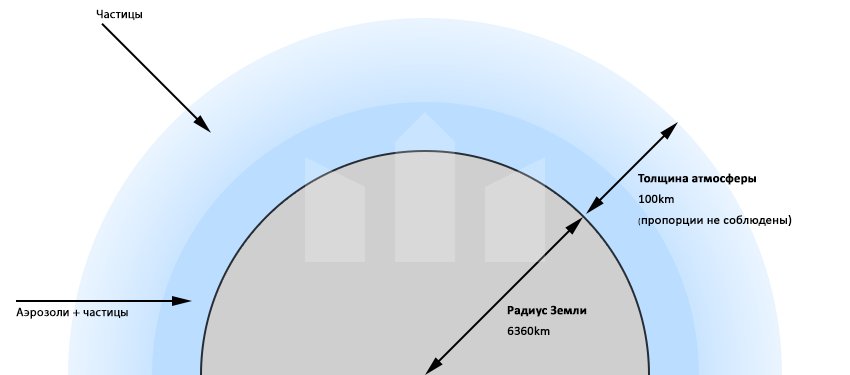
Атмосфера планеты тоже непрозрачная – распространяясь в этой непрозрачной среде свет сталкивается с микрочастицами, аэрозолями (об этом ниже) претерпевая изменения на пути от солнца к наблюдателю. Толщина атмосферы определяется линией Кармана – высотой в 100км над уровнем моря. Эта высота считается верхней границей атмосферы и является границей между атмосферой Земли и космосом.
Существующие подходы
На момент написания статьи существует два подхода для расчёта эффекта атмосферного рассеяния:
-
Подход Nishita, описанный в двух статьях: «Display of the Earth Taking into account Atmospheric Scattering» (1993) и «Display of the Earth Taking into account Atmospheric Scattering» (1996)
-
Подход Preetham, описанный в статье «A Practical Analytic Model for Daylight» (1999)
В этот статье мы будем рассматривать модель атмосферы от Nishita. Следует заметить, что описанные выше алгоритмы не менялись существенно с момента их изобретения и применяются до сих пор. Различается только их реализация: на текущий момент времени есть много способов ускорить работу этих, достаточно требовательных с вычислительной точки зрения, алгоритмов.
Модель атмосферы
Как известно, атмосфера планеты состоит из частиц. Сталкиваясь с этими частицами луч света (а на самом деле э/м волна) отклоняется от своего исходного направления. Этот процесс может происходит многократно, и именно он называется атмосферным рассеянием, то есть рассеянием света в атмосфере планеты.
Как уже говорилось выше, атмосфера планеты имеет толщину в 100км. Для начала стоит учесть, что плотность атмосферы разная на разной высоте. В большинстве моделей считается, что плотность атмосферы меняется экспоненциально:
В приведённой выше формуле density(0) – плотность атмосферы на уровне моря, H – толщина атмосферы, h – высота, для которой рассчитывается плотность атмосферы.
Далее в модель атмосферы вводятся частицы, из которых состоит атмосфера, и аэрозоли – частицы большего размера, присутствующие только на нижних слоях атмосферы.
Рассеяние света, происходящее при столкновении с маленькими частицами (присутствующими во всей толще атмосферы) называется Рэлеевским рассеянием (Rayleigh scattering). Рассеяние света, происходящее при столкновении с аэрозолями называется рассеянием Ми (Mie scattering). В результате, из двух видов рассеяния и складывается итоговая модель атмосферы Нишиты (Nishita).
Рэлеевское рассеяние
Как уже говорилось выше, Рэлеевское рассеяние – это рассеяние света, происходящее при столкновении с частицами, из которых состоит атмосфера. Доля энергии, которая теряется при столкновении с одной частицей, называется коэффициентом рэлеевского рассеяния (или коэффициентом затухания), и вычисляется по следующей формуле:
В приведённой выше формуле:
- λ – длина волны
- h – высота над уровнем моря
- n – коэффициент преломления воздуха (1.00029)
- N – количество молекул на кубический метр стандартной атмосферы (2.504 * 1025)
- HR – коэффициент масштабирования (обычно берётся в пределах 8-9 км)
Обратите внимание, что в приведённой выше формуле длина волны присутствует в знаменателе, т.е. чем больше длина волны, тем меньше энергии будет потеряно при столкновении с частицей атмосферы. Рассмотрим следующие значения длин волн: 440нм, 550нм, 680нм. Эти длины волн – пиковые значения для синего, зелёного и красного цветов соответственно.
Таким образом, синяя составляющая рассеивается гораздо сильнее, чем красная, что особенно видно, когда световые волны проделывают долгий путь сквозь атмосферу: на закате. Именно этим объясняются оранжево-красные цвета неба на закате.
Для ускорения расчётов вместо всего видимого спектра длин волн будут использоваться только три пиковых значения (440нм, 550нм и 680нм), а в качестве высоты можно выбрать уровень моря. Таким образом становится возможным предрассчитать коэффициенты рэлеевского рассеяния для RGB компонент и использовать их в шейдере в виде константы, чтобы получить близкие к реальным цвета неба, не потеряв при этом в скорости работы алгоритма.
Далее вводится понятие фазовой функции. Эта функция задаёт зависимость между направлением рассеяния и долей света, утерянной в этом направлении. Обозначим угол рассеяния как θ тогда фазовая функция для Рэлеевского рассеяния будет выглядеть так:
где
С использованием фазовой функции и коэффициента рассеяния формируется итоговое уравнение рэлеевского рассеяния, обозначающего долю рассеянного в направлении θ света с длиной волны λ на высоте h:
Рассеяние Ми
В нижних слоях атмосферы требуется учитывать уже не только частицы, из которых состоит атмосфера, но и т.н. аэрозоли (частицы, размер которых больше чем длина волны, например смог или пыль). Алгоритм расчёта тут такой же, как и для Рэлеевского рассеяния, меняются только формулы для коэффициента рассеяния и фазовой функции. Коэффициент рассеяния Ми рассчитывается по следующей формуле:
В приведённой выше формуле:
- λ – длина волны
- h – высота над уровнем моря
- HM – коэффициент масштабирования (для рассеяния Ми обычно принимается равным 1.2 км)
- β(λ,0) – предрассчитанное значение коэффициента рассеяние, замеренное на уровне моря (21e-6)
Фазовая функция для рассеяния Ми выглядит следующим образом:
Обратите внимание, что в функции появилась новая переменная - g. Эта переменная называется коэффициентом анизотропии, и для земной атмосферы её значение принимается равным 0.76.